Stories as Proofs

I’ve been exploring a few different facets of logic programming for generative writing, simulation and world building. I’m not a theorist and struggle with understanding and manipulating concepts using formal logic—perhaps more than I should. But that’s exactly why I’m challenging myself to dig deeper here. My primary interest in exploring research like this is to look for potential applications and opportunities to open up these capabilities to authors who don’t have a computer science or mathematical logic background.

One of the more innovative ideas I’ve come across is the use of a distinct form of formal logic called linear logic as a tool for representing narratives and generating stories.

Linear logic is distinct from classical logic in that it doesn’t deal with the truth of propositions, but with the availability of resources. Instead of facts that remain true and can be used to derive other facts or be ignored, resources can be consumed or modified but they cannot be duplicated or discarded.

The idea of applying this form of logic to narrative generation was first proposed in Linear Logic for non-linear storytelling, then explored in more detail in Linear Logic Programming for Narrative Generation by Chris Martens, Anne-Gwenn Bosser, João F. Ferreira, and Marc Cavazza.

We use the language Celf to represent narrative knowledge, and its own querying mechanism to generate story instances, through a number of proof terms. Each proof term obtained is used, through a resource-flow analysis, to build a directed graph where nodes are narrative actions and edges represent inferred causality relationships. Such graphs represent narrative plots structured by narrative causality.

Taking the major causal links from the plot of Flaubert’s classic novel Madame Bovary, the authors show how to encode these plot elements in linear logic to generate hundreds of new story variants that are consistent with the events of the original story.

Examples of the narrative actions for Madame Bovary are included in the paper, but you can also look an updated version of the entire program on GitHub. Like most logic programming languages, the terse syntax belies its considerable expressive power.

While related to propositional approaches to narrative generation using forward or backward chaining, the linear logic structure of actions producing and consuming resources makes it possible to model repeating actions or qualities that increase or decrease. This would be really difficult to achieve using classical logic.

The argument for linear logic here is that it provides an explicit representation of the semantics of action and change. When applied to Madame Bovary, it allows for higher level abstractions of driving forces in the story like Emma’s desire to escape boredom.

What does this look like in practice?

The narrative program has two main constructs: resources, which include characters, states and qualities found in the story, and actions, which are transforming events that produce and consume resources.

Looking at the program, we start by observing that the goal, emmaCharlesMarried, can only be produced by the action emmaMarries. Moreover, this action requires the existence of the resource grace, which can only be produced by the action emmaSpendsYearsInConvent. As a result, all the graphs will have the action emmaSpendsYearsInConvent as a predecessor of the action emmaMarries. On the other hand, the resource escapism can be produced by two different actions: emmaGoesToBall and emmaReadsNovel. This means that in some of the generated stories, the action emmaMarries can choose between the resource produced by these two actions.

With this setup, it’s possible to run queries that trace a causal path through resources and actions to reach a given goal state, which corresponds formally to a proof search. To use this system for narrative generation, we simply need to record each step taken in the proof and treat it as a causal link in the story.

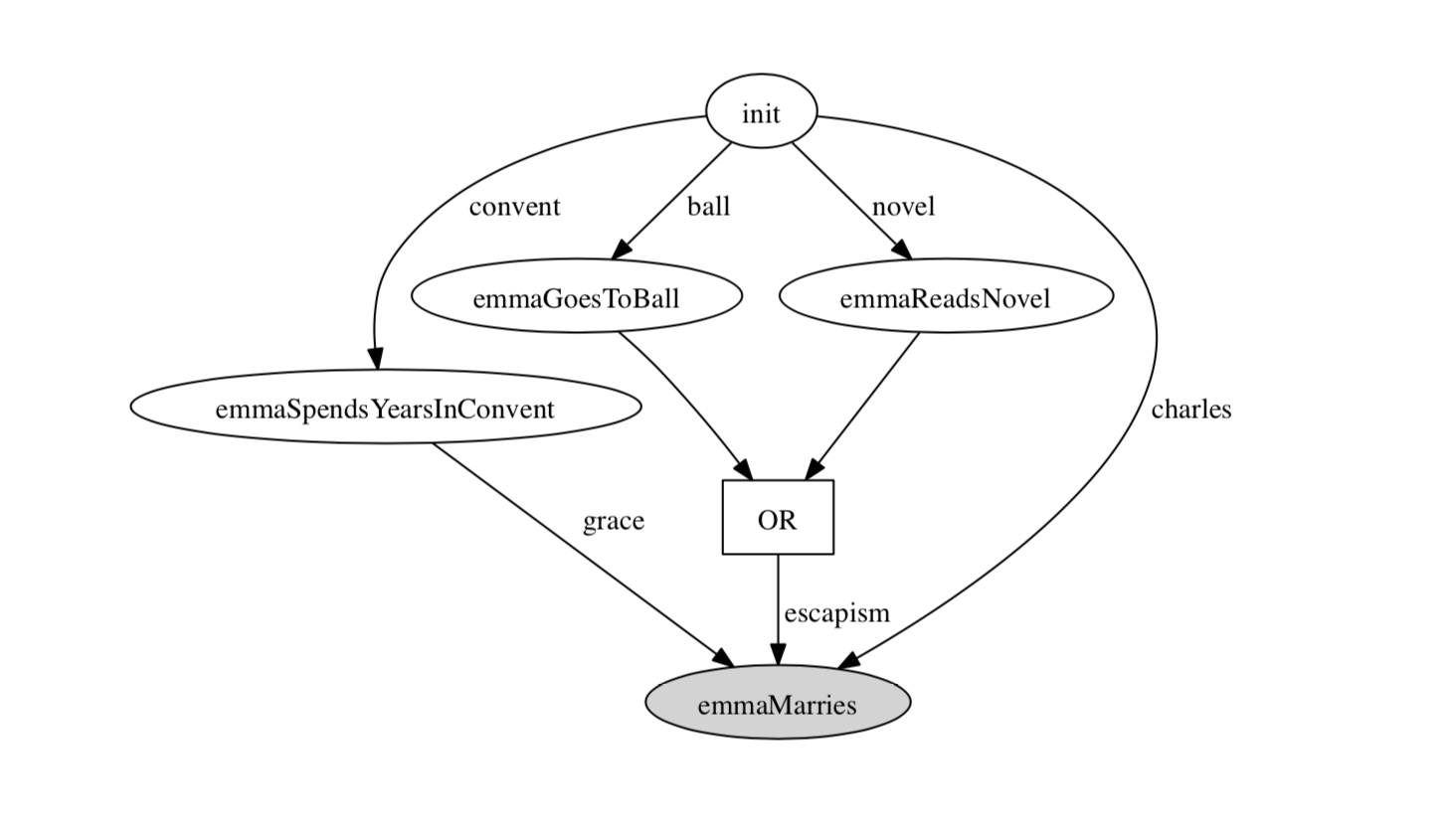
To generalise a common set of stories that have a beginning, middle and end, the convention is to specify an initial state with resources and actions that provide a consistent starting environment.

Despite expressing only one branching choice explicitly (whether or not Emma attends the Vicomte’s ball), the given encoding of Madame Bovary leads to a surprisingly large variety of causally-linked plots able to be generated.

When requesting 1000 query attempts, we obtain 747 solutions, among which 697 are different narrative sequences, and 226 are different plots (i.e., 226 true story variants).

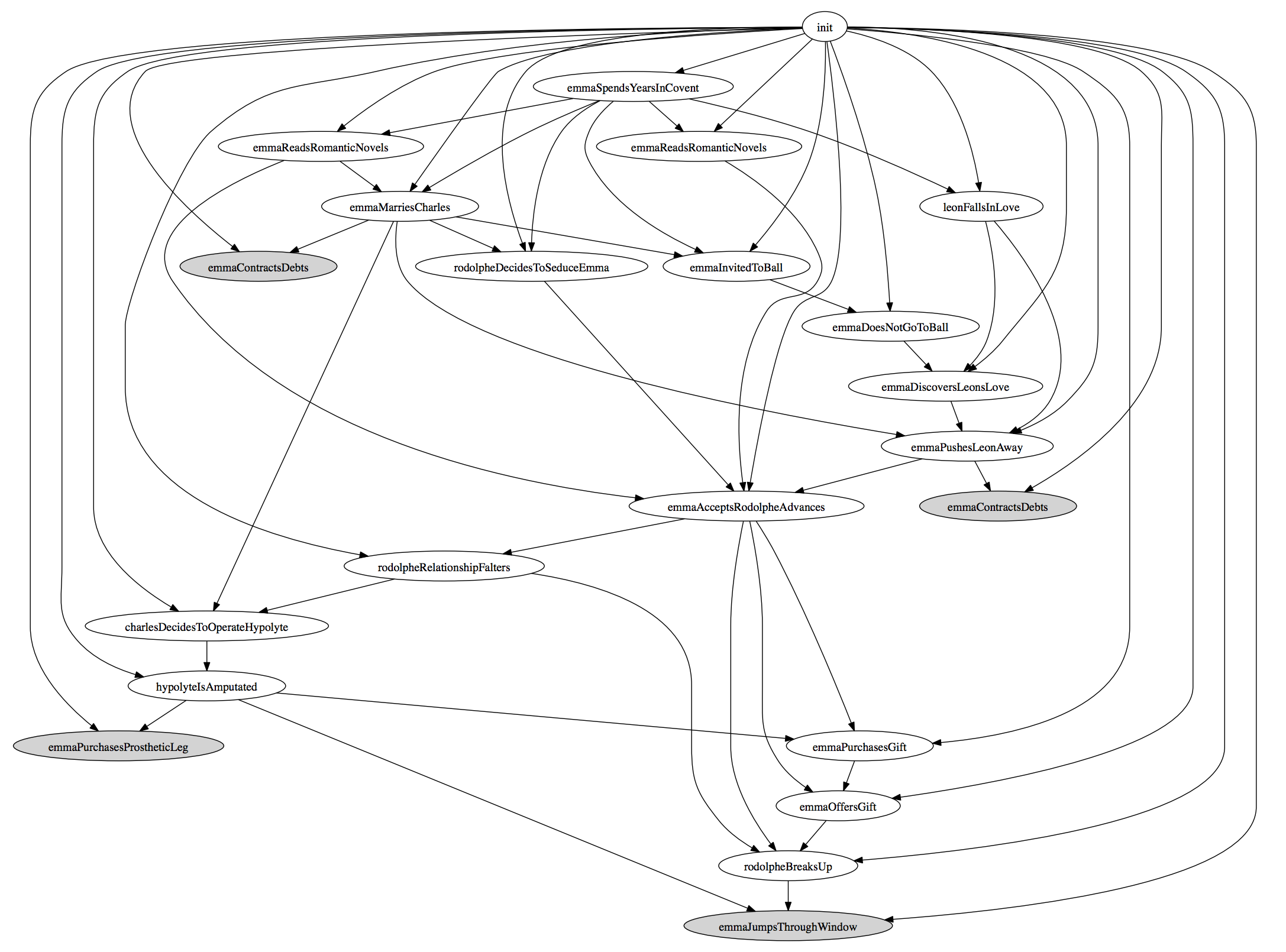
In the following example taken from the paper, Emma does not attend the Vicomte’s Ball but still wants to escape her life and defenestrates when Rodolphe leaves her.

In a subsequent paper Generative Story Worlds as Linear Logic Programs, the authors extend this approach to story worlds that support many different characters, interactivity, and feedback loops.

Similar to the narrative of Madame Bovary, story worlds are built from two primary constructs: resources which are predicates representing states or qualities of the world, and actions which are ways in which the world state can be changed by producing and consuming resources.

They give an example of a Shakespearean romantic tragedy story world (source code on GitHub).

The state we model includes sentiments between characters (several forms of love and hate), physical locations and basic movement, possession of key objects (such as weapons), relationship states (marriage and being single), desires for objects, and solitary emotions (depression).

The authors suggest that the particular set of predicates chosen have an influence akin to genre. This decision process also involves deciding whether to contradict or enforce social norms.

The delineation of the story world into predicates is an act of careful human design, often iterated with the generation of stories, and the choices made here make all the difference in terms of which actions are possible to write and therefore what shapes the story can take. For instance, the choice to include two kinds of love, eros and philia, means that we can codify social rules about sexual relationships between characters. Similarly, the choice not to include a predicate for a character’s gender renders it impossible to enforce heteronormative relationships.

So how do the stories end? If each character action requires at least one character to be alive, then searches through the story space will automatically terminate when all the characters are dead. Since this is exhaustive and bordering on the ridiculous—even for Shakespeare—the authors show how to introduce rules that lead to a final state from desired end conditions, meaning that different dramatic possibilities can be tagged as endings, allowing for a wider range of possible story outcomes.

If you’re familiar with partial order planning, you will notice a lot of similarities in structure: the initial state, goal state, actions and predicates all have direct correspondences in plannng methods. As far as I can understand, the approach using linear logic is distinguished by being purely functional and declarative. Searching and evaluation is handled by the programming language itself, rather than data structures and algorithms embedded in a general-purpose imperative language.

One of the benefits of the narrative structure corresponding directly to a formal logic is that different use cases can be supported by the same underlying execution model. Not only does this approach enable random generation of narratives that are causally coherent according to the given system of rules, it also allows narratives to be verified and checked to avoid gaps and holes and ensure that they satisfy desired constraints for stories and game mechanics, almost like a game design version of a proof assistant.

The takeaway point of this paper is that encoding story worlds in a linear logic programming language allows for informative exploration of their consequences. Two of these exploration techniques are random story generation and structural analysis, and what enables those techniques to fall naturally out of our encoding is the fact that there is a direct and formal correspondence between stories and proofs.

Chris Martens has since taken this research even further, developing tools like Ceptre, a linear logic environment designed to support development and testing of interactive and generative narratives and games (source code on GitHub).

Despite my difficulty with the somewhat bewildering set of new formalisms and unfiltered algebraic syntax, it’s clear that both linear logic and the broader methodology of interactive exploration tools based on proofs as constructions has huge potential. I will be fascinated to see how this develops.