What Makes a Generator Interesting?

Scott Turner, author of Dragons Abound describes an intriguing mental model that he calls ‘Interesting Space’, building on the definitions of ‘Possibility Space’ and ‘Generative Space’ documented by Mike Cook.

Possibility space is the set of all possible outputs we can describe, given the output form of a generator (imagine Minecraft worlds made up entirely of flat grass or Dwarf Fortress maps containing nothing but andesite rock and pools of magma). On the other hand, generative space is the actual set of outputs that a generator can produce.

Which leads to the following design questions for any given generator:

• Which areas of the possibility space are interesting?
• How do they intersect with the generative space?

A fairly intuitive idea is that good generators have a large overlap with interesting space, wheras bad generators don’t.

These potential overlaps are easiest to explain visually.

I think it makes sense to think about the Generative Space as a connected, compact region. But I think drawing the Interesting Space the same way is probably exactly wrong. It should be drawn as a scattered, disjoint set of weirdly-shaped areas. Why? Because (1) things can be interesting for different, orthogonal reasons, and (2) interestingness is a discontinuous function. These things together suggest that we ought to draw the Interesting Space as a bunch of disjoint, oddly shaped regions.

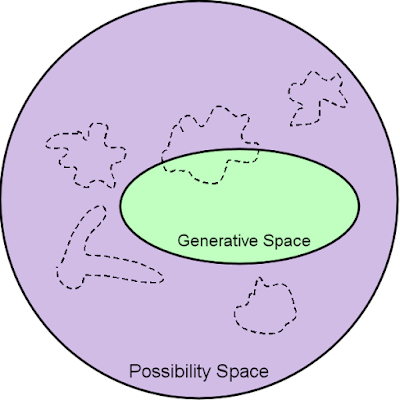
This explains at a glance why procedural generation is so difficult. Building generators that can hit these small and widely dispersed targets involves extensive research and design work, a deep knowledge of the domain and well-defined goals for the output. Turner explores this with a salient critique of the Perlin noise based approaches which have infected the entire gaming and simulation community.

Underpinning all this is the research by Gillian Smith on understanding generators as a whole by formalizing the qualities of generative spaces into metrics that can be used to explore the overall range of output of generators, rather than just running them over and over and manually perusing the individual outputs.

The idea is that by carefully specifying design constraints and desired output qualities as metrics, we can move from metaphors and conceptual models of nested sets to actual statistical data and visualisations with concrete insights and automated critiques of generators in operation—maybe even leading to tools for tweaking and improving the generators at the generative space level.