The Axes of Parsing

		<p>This is an introductory guide to the theory and praxis of parsing and lexical analysis. All this material is a necessary basic foundation for building domain specific languages, compilers, and much more.</p>

This article covers the basic theory of formal languages and explain the fundamental concept of grammars, and their symmetry with regular expressions and finite state machines.

This is not a topic that you can just absorb passively. I recommend grabbing a pad and pencil and writing out some of the example sets, so that you see intuitively how the relations work (for a refresher on the syntax used in this article, see Describing Sets).

Alphabets and Languages

Let Σ be an alphabet - a finite set of symbols. One of the most simple examples is Σ = {0, 1} - the binary alphabet. Members of an alphabet are known as letters or symbols. Words or strings over an alphabet are combinations of these symbols in the set. Using the example of the binary alphabet - 00, 01, 110, 1111 are all strings over this alphabet. The set of all strings over the alphabet is usually denoted Σ*. This set includes the empty string, ε which is the word of length 0 that is common to all alphabets.

A language L over an alphabet Σ is a subset of Σ*. Languages are defined by a particular set of syntactic rules that determine whether a string in Σ* is accepted or rejected by the language. One way of defining a language is simply to list all the words in the language - but this will not always work, as many languages are infinite even if they have a finite alphabet (eg: L = Σ*, where Σ = {0, 1} is the language with infinitely many combinations of 0 and 1).

Defining a Language with Grammars

There are several formalisms that provide a mechanism for defining a language, and these formalisms interlock to form the foundation of many important aspects of computer science. The two basic formalisms we are concerned with here are grammars and regular expressions. It's worth noting that these definitions of a language are purely syntactic constructions - they do not have anything to do with meaning. In theory, the language is just a structure. Meaning is separate, and unrelated to the definition of the language itself.

A formal grammar is a set of production rules for transforming strings, and a finite set of non-terminal symbols (corresponding to productions) and terminal symbols (corresponding to the alphabet Σ). Beginning at a start symbol S, the production rules are applied in sequence to rewrite non-terminal symbols into terminal symbols to produce a string. The set of all strings that can be generated by these productions defines the language L. The grammar G is defined as G = {N, Σ, P, S}:

An example grammar might be:

• N = {S, Z} - the set of non-terminals
• Σ = {0, 1} - the alphabet

The set of production rules P defines a mapping from the non-terminals to productions, where S is the start symbol:

1. S → 0Z
2. Z → 1Z
3. Z → ε

Looking carefully, you'll notice that Z is recursive because it appears on the right hand side of its own production. This is a very important aspect of how grammars work. Non-terminals with multiple productions like this are commonly abbreviated on a single line, like: Z → 1Z | ε.

To test if a string is accepted by G, we begin at the start symbol and rewrite the non-terminals until the productions are exhausted. For example, if we feed in the strings ε, 0, 00, 01, 011, 0110 to the above grammar, we get the following results:

• ε cannot be accepted by the starting production S → 0Z, which expects at least one 0, so the string is rejected.
• 0 maps to S → 0Z, and Z can be rewritten to the empty string using Z → ε, so the string is accepted.
• 00 maps to S → 0Z, but when we rewrite to follow Z → we find that neither production of Z will accept 0, therefore the string is rejected.
• 01 maps to S → 0Z and follows to Z → 1Z. Since 01Z can be consumed by Z → ε this produces 01 so the string is accepted.
• 011 maps to S → 0Z and follows to Z → 1Z, which rewrites to 01Z. Following Z → 1Z again produces 011, so the string is accepted.
• 0110 rewrites as far as 011Z0 but neither production of Z will accept the trailing 0 so the string is rejected.

Systems like this are classified under the broad category of generative grammars. They were first studied in the mid 20th century by Noam Chomsky, but also have precedents in earlier work by Emil Post on computational systems and string rewriting. We'll return to look at the significance of Chomsky's discoveries later on. But first, we need to contrast grammars with the formalism of regular expressions.

Defining a Language with Regular Expressions

Regular expressions are pattern based methods of string matching. Like grammars, they can be used to define a given language by determining whether a given string is accepted or rejected. The difference being that regular expressions match a string against a literal pattern, rather than rewriting a series of recursive productions. Formally, a regular expression consists of constants (symbols) that denote sets of strings and a group of operators that work over these sets.

For the alphabet Σ, the following constants are defined:

• ∅ denoting the empty set
• ε denoting the empty string
• A...Z literal characters belonging to Σ

And the following operations are defined:

• concatenation - A.B which combines strings from two sets into single strings
• alternation - A∪B which denotes the union of strings from two sets
• Kleene closure or star - A* which denotes the set of all strings that can be made by concatenating zero or more strings from A

Some examples of regular expressions over an alphabet Σ = {a, b} are:

• a.b = { ab }
• a*b = { b, ab, aab, aaab, ... }
• a∪b* = { ε, a, b, bb, bbb, ... }

The regular expression that accepts the same language as the above grammar defined for Σ = {0, 1} is: 01*.

Note that the regex pattern matching syntax found in most modern programming languages is a super-set of this basic formalism. It's common to find variations of this syntax using the conventions ab for concatenation and a|b for alternation. The * sigil is generally used to match 0-or-more characters (a Kleene closure), with the variation + for 1-or-more characters. It's important to note that these regex libraries in popular programming languages have a much broader expressive power than the regular languages we are discussing here. We will revisit this point soon, once we have outlined exactly what a regular language is.

The regular expressions were first invented and studied by Stephen Kleene, whose name is given to a number of related mathematical concepts including the Kleene closure. Intuitively, we can see that grammars and regular expressions are both different methods of achieving the same result - recognizing whether a given string belongs to a language. But no matter how obvious, such a vague correspondence is unsatisfying for mathematicians, who seek a more rigorous determination of this result. And as it turns out, searching for a proof of this equivalence yields one of the most stunning and satisfying symmetries in the realm of computer science and mathematics.

Defining a Language with State Machines

Bringing this together requires diving below the realm of syntax to find a deeper construct that is capable of unifying these formalisms. What we need is a particular type of abstract machine that is capable of accepting input and deciding whether or not the input belongs in a given language. Generally, these kinds of constructs are known as finite state machines or finite automata, and here we are concerned with two particular kinds - deterministic finite automata (DFA) and non-deterministic finite automata (NFA). In essence, an automaton is an abstract flow chart consisting of various particular states, and transitions that link between those states. At any moment in time, the automaton MUST be in one of its states. This construct can be used as a string recognizer by allowing its states to represent particular sequences of input symbols, with the transitions enabling the machine to read accept further input sequences.

The key difference between a DFA and an NFA is the way that the transitions connect between the various states. As the name suggests, a deterministic automaton has a unique transition from each possible state. A non-deterministic automaton can have several different transitions from each possible state.

To use an automaton to model a string recognizer we need to know how the machine can start and stop. To do this, we label a starting state where input begins and an accepting state where it is valid for the machine to halt. The conventions used to denote these concepts in diagrams are to place an arrow from nowhere pointing to the starting state and to label the accepting states with a double circle.

To function as a recognizer for a language, the automaton must consume every character in the given string, and finish on an accepting state when the last character is consumed. If the input does not end on an accepting state, the string is rejected.

The following diagram illustrates an automaton that accepts the same language as 01*. The first transition from S1 to S2 occurs when the input 0 is consumed. S2 is an accepting state, with a transition on 1 that loops back to itself, therefore representing the Kleene closure, being able to consume zero or more instances of 1 before halting:

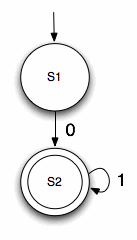<p>This automaton is classified as a DFA because there is exactly one transition out of each possible state.</p>

Another way of representing this automaton is to create a state transition table which maps the various states and possible transitions between them. The equivalent table to 01* looks like:

	0	1
S1	{S2}
S2		{S2}

NFAs differ from DFAs in that they allow multiple transitions out of a given state. One class of NFAs can even include transitions between states without consuming any input - these are known as epsilon transitions or lambda transitions. In 1959, Michael O. Rabin and Dana Scott published Finite Automata and Their Decision Problem, where they introduced the concept of NFAs and showed that mathematically, for any given NFA there is an equivalent DFA. Any NFA can be converted into a DFA using the powerset construction. This algorithm forms the basis of regex pattern matching implementations in many programming languages. In a subsequent article, we will look at how to implement a language recognizer using an NFA to DFA conversion.

Symmetry of Regular Languages

All these relationships prove to be very useful in establishing a precise definition of formal languages. A regular language is thus defined as a set of strings from a finite alphabet that satisfy the following conditions:

• it is accepted by a deterministic finite automaton
• it is accepted by a non-deterministic finite automaton
• it is described by a regular expression
• it can be generated by a regular grammar

The astounding symmetry is that all these constructions represent exactly the same set of possible languages. The discovery of the equivalence of finite automata and regular expressions provided a context for understanding previous work by Noam Chomsky who published Three models for the description of language in 1956, where he first outlined the concept of a hierarchy of languages generated by formal grammars. Regular grammars, thus emerged as the class of grammars that are equivalent to regular expressions and finite automata, where the productions are restricted to allowing only a single non-terminal on the left hand side of the production, and only allowing a single terminal and non-terminal or the empty string on the right hand side.

Hierarchy of Grammars

Chomsky defined four types of grammars in the hierarchy, of which, the regular grammars were classified as the most restricted. The other types are context free grammars, context sensitive grammars, and recursively enumerable grammars:

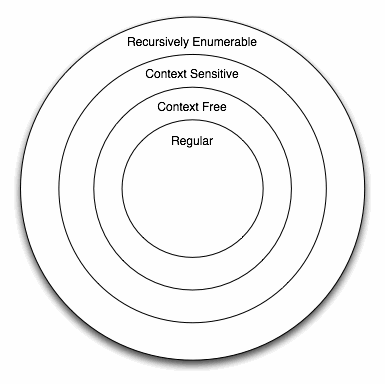<p>A context free grammar is a grammar where the left hand side of every production rule is a non-terminal, and the right hand side is any combination of terminals and non-terminals or the empty string. This is a wider class of grammars than regular grammars, but it is important to note (based on the hierachy) that every regular grammar is context free. Chomsky described context free grammars as phrase-structure grammars. While this formalism was originally developed for studying linguistics and natural language, it has had a far greater impact on the development of programming languages through the field of lexical analysis.</p>

A Syntax for Representing Context Free Grammars

The first programming language to be specified by a context free grammar was Algol 58, which used a meta-syntax designed by John Backus and later improved by Peter Naur for Algol 60. This meta-syntax is now known as Backus-Naur Form or BNF and is widely used to generate code for parsers based on a grammar specification.

BNF uses the same basic production rule format as the regular grammars described above, with the right side being a substitution for the symbol specified on the left side:

<NON-TERMINAL> ::= EXPRESSION

Where EXPRESSION is a combination of terminal and non-terminal symbols, and alternation is specified by |. An example BNF version of the binary language 01* described in the previous examples would be:

<S> ::= "0" <Z>
<Z> ::= "1" <Z> | ""

Another example would be a production defining the available symbols in the set of Arabic numerals:

<digit> ::= "0" | "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9"

There are many different flavors and extensions of BNF, but all are based on the same basic concept of a block structured grammar.

Why is this important?

If you understand BNF, there are many tools you can use to generate parsers by specifying the exact grammar you want to interpret. Understanding the mechanics of syntax, regular expressions, and formal languages is an essential milestone in mastering the art of programming. The general concepts are applicable across a broad range of programming domains.

Part I of a work in progress.